परिमेय संख्‍याओं और पूर्णांक में अंतर समझिये

 पूर्णांक का शाब्दिक अर्थ है पूर्ण शब्‍द, यह फर्क नहीं कि यह एक धनात्‍मक संख्‍या है अथवा एक ऋणात्‍मक संख्‍या। पूर्णांक को अंग्रेजी में इंजीजर (integer) कहते हैं जो एक लैटिन भाषा का शब्‍द है जिसका अर्थ है Whole Number (पूर्ण संख्‍या).  दरअसल जब मैं स्‍कूल के छात्रों को पढ़ा रहा था तो मैंने देखा कि कई विद्यार्थियों को परिमेय संख्‍याओं अथवा पूर्णांक आदि के बारे में साधारण जानकारी का अभाव है, तो दूसरी तरफ ऐसे भी कई सारे छात्र रहे हैं जिन्‍हें पूर्ण संख्‍या, प्राकृत संख्‍या अथवा पूर्णांक के साथ - साथ परिमेय / अपरिमेय संख्‍या के परिभाषा के बारे में पता था, परन्‍तु असल में इनके मायने क्‍या हैं, यह पता नहीं था। 

आज इस लेख में हम पूर्णांक और परिमेय संख्‍याओं के बारे में साधारण शब्‍दों में अध्‍ययन करेंगे। इस लेख में आप जान पाएंगे कि पूर्णांक और परिमेय संख्‍याएं किस प्रकार से एक दूसरे से भिन्‍न हैं। पूर्णांक समझने से पहले हम प्राकृत संख्‍याओं और पूर्ण संख्‍याओं को भी समझ लेंगे। हालांकि कुछ गणितज्ञ पूर्ण संख्‍या को प्राकृत संख्‍या ही मानना पसंद करते हैं अथवा पूर्ण संख्‍या अथवा प्राकृत संख्‍या में अंतर का मायना नगण्‍य होने पर बल देते हैं। 

प्राकृत संख्‍या (Natural Numbers) - ऐसी संख्‍याएं जो गणना के लिए प्रयुक्‍त की जाती हैं। यह साधारण तौर पर 1,2,3,4 ..... अनंत आदि संख्‍याएं होती हैं, जो वस्‍तुओं के गणना के लिए प्रयुक्‍त की जाती हैं। जैसे - 2 पेन, 4 पेन, 6 आलमारी, 4 मोबाईल फोन आदि। 

पूर्ण संख्‍या (Whole Numbers) - प्राकृत संख्‍याओं में 0 को भी यदि शामिल कर लिया जाए तो वह पूर्ण संख्‍या बन जाती है। कुछ गणितज्ञ पूर्ण संख्‍या को प्राकृत संख्‍या का ही भाग मानते हैं क्‍योंकि प्राकृत संख्‍या में 0 (शून्‍य) को यदि शामिल कर लिया जाए तो यह पूर्ण संख्‍या बन जाती है। 

पूर्णांक (Integers) - संख्‍या रेखा का अध्‍ययन करने पर हम प्राकृत संख्‍याओं के विपरीत ऋणात्‍मक संख्‍याएं भी प्राप्‍त करते हैं। ऋणात्‍मक संख्‍याओं, शून्‍य (0) और धनात्‍मक प्राकृत संख्‍याओं को एक साथ हम पूर्णांक के दायरे में रखते हैं। ध्‍यान देने योग्‍य बात है कि पूर्णांक/पूर्ण संख्‍या/प्राकृत संख्‍या का पूर्ण संख्‍या (अर्थात् दशमलव न हो) होना आवश्‍यक है। पूर्णांक - -1, -2, -3, .... , 0, 1, 2, 3 आदि। ध्‍यान रहे कि दशमलव में आने वाली संख्‍याएं पूर्ण संख्‍या नहीं होती हैं, अत: ये संख्‍याएं पूर्णांक नहीं होती हैं। 

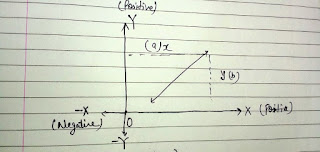
संख्‍या रेखा का अध्‍ययन

परिमेय संख्‍याएं (Rational Numbers) - ऐसी संख्‍याएं/अंक जिन्‍हें अंश / हर के रूप में लिखा जा सके और जहां हर का मान 0 न हो, परिमेय संख्‍याएं कहताली हैं। इसमें दशमलव संख्‍याएं भी आती हैं जो दशमलव के बाद किसी स्‍थान पर जाकर शांत हो जाए। जैसे 3.5 भी एक परिमेय संख्‍या है जिसे 35/10 के रूप में लिखा जा सकता है। दूसरी तरफ 3.5 को संख्‍या रेखा पर एक निश्चित बिन्‍दु पर निर्धारित किया जा सकता है। 

अपरिमेय संख्‍याएं (Irrational Numbers) - ऐसी संख्‍याएं जिन्‍हें अंश / हर के रूप में न लिखा जा सके, दूसरे शब्‍दों में जिसका मान संख्‍या रेखा में निश्चित बिन्‍दु पर प्रदर्शित नहीं किया जा सके, अपरिमेय संख्‍याएं कहलाती हैं। अभाज्‍य संख्‍याओं के वर्गमूल का अध्‍ययन करने पर पाया गया कि उनका मान दशमलव के बाद किसी भी निश्चित स्‍थान पर शांत न होकर आगे बढ़ता रहता है (जैसे - 1.7345246332433234 .............. ) , इसलिए √अभाज्‍य संख्‍याएं अपरिमेय होती हैं। 

साधारण शब्‍दों में कहें तो परिमेय संख्‍याएं वह संख्‍याएं होती हैं जिनका निरूपण संख्‍या रेखा पर सटीक किया जा सके, वहीं अपरिमेय संख्‍याएं वह संख्‍याएं होती हैं जिनका निरूपण संख्‍या रेखा पर सटीक बिन्‍दु पर न किया जा सके। 

उम्‍मीद है आपको यह लेख पसंद आया होगा। हम इसी तरह के महत्‍वूर्ण लेख लाते रहेंगे, आप हमारे साथ बने रहिएगा।

गणित का जादू : आइये सीखें एवं दोस्‍तों को चौकायें (Magic of Mathematics : Let's learn and surprise your friends)

 दोस्‍तों, आपने कई बार जादू देखे होंगे। ऐसे जादू जो कि लोगों को गायब कर दे, कागज़ में बिना माचिस के आग लगा दे, हाथ घुमाकर माला पहना दे और न जाने कितने तरह के जादू होते हैं। आपने कई बार सोचा होगा कि चलो हम भी जादू सीखते हैं व लोगों के नज़र में आते हैं। परन्‍तु इस जादू के लिए तंत्र - मंत्र सीखना होगा हम ऐसा सोचकर रह जाते हैं। हमें याद है कि टीवी में तंत्र-मंत्र सुनकर अकेले में हम भी दोहराते हैं कि कहीं वह सच तो नहीं, परन्‍तु अब चमत्‍कार होना बन्‍द हो गया हो, मानो ऐसा प्रतीत होता है और उलझन भी होती है।

magic of mathematics

अरे, कोई बात नहीं, टीवी वाले चमत्‍कार भले ही झूठे हों परन्‍तु विज्ञान का चमत्‍कार हमेशा सच ही होता है। आज हम आपको ऐसी ट्रिक बताने वाले हैं कि आप अपनी कक्षा में, अपने दोस्‍तों के बीच या कोचिंग सेंटर या ऑफिस में गणित का जादू दिखाकर सबकी वाहवाही पा सकते हैं। तो आइये सीखें गणित का जादू- 

नियम - गणित के इस जादू में आपको अपने दोस्‍त से 3 अंको की संख्‍या पूछनी है। वह संख्‍या बतायेगा तो आप उसका उत्‍तर पहले ही लिए देंगे, और उससे कहेंगे कि एक बार फिर वह 3 अंको की संख्‍या बाले, फिर आप उसके बाद एक संख्‍या लिखेंगे, फिर एक बार वह बोलेगा और आप अपने मन से एक संख्‍या लिखेंगे और देखेंगे कि उत्‍तर जोड़ने पर उतना ही आयेगा जितना आपने बोला था।

नोट - इस प्रक्रिया में आने अपने दोस्‍त से 3 बार संख्‍या पूछा व अपने से 3 बार संख्‍या लिखा। आपने पहली बार दोस्‍त के संख्‍या के बोलने के बाद उत्‍तर लिख दिया, फिर दोस्‍त ने बोला फिर आपने लिखा यह प्रक्रिया दो बार दोहरानी है। अरे, टेंशन मत लो, बहुत आसान है। तो चलिए शुरू करते हैं गणित का जादू - 

---

स्‍टेप 1- दोस्‍त से तीन अंको कि संख्‍या पूछिए । माना कि उसने बोला 470

स्‍टेप 2- अब आपको उत्‍तर लिखना है। उत्‍तर लिखने कि लिए उस अंक से पहले 2 लिख देना है व जो मूल अंक है उसमें से 2 घटा देना है। 470 - 2 = 468 (अब 468 के पहले 2 लिए देना है) इसलिए उत्‍तर होगा 2468

स्‍टेप 3- अब दोस्‍त कोई 3 अंकों की संख्‍या फिर से बोलेगा। माना उसने बोला 536 

स्‍टेप 4- इसके बाद आपको अपने से 3 अंकों की संख्‍या 536 के नीचे लिखनी है। आपको संख्‍या सोचनी नहीं है, बल्कि ऐसी संख्‍या लिए दीजिए की 536 में प्रत्‍येक जातीय संख्‍या के आमने सामने के अंकों का योग 9 हो। 536 के नीचे आपको 463 लिखना होगा, क्‍योंकि 5+4=9, 3+6=9, 6+3=9 तो इस प्रकार से आपको एक बार और दोहराना होगा। यदि किसी संख्‍या में 0 लिखा हो तो उसके सामने आपके 9 लिख देना है।

स्‍टेप 5- अगली बार इसी प्रकार आपके दोस्‍त ने संख्‍या 790 बोला, तो आप उसके बाद लिख देंगे 209 (ऊपर स्‍टेप 4 का नियम देखिए)

स्‍टेप 6- अब उन सभी संख्‍याओं को जोड़ दीजिए जो आपके दोस्‍त ने 3 बार बोला व आपने, उत्‍तर के अलावा, जो दो बार लिखा जिससे जातीय संख्‍याओं का योग 9 आए। 

470+536+463+790+209 = 2468

क्‍यों, मान गए न गुरू ? तो अब देर किस बात कि? आज कि अपनी कक्षा में जाओ और दिखा दो गणित का जादू। 

Line Passes Through Two Lines

 Generally in Competitive exams questions are being asked from linear equation. A line's equation is always a linear equation. So in this article you are going to know basics of lines and other relevant facts. So let's start!

Linear Equation - An equation consists of two variables X and Y that denotes the position and direction of that line in Axis graph chart.

For example, ax+by+c=0 is an equation. It means the direction of the line is a unit towards X-Axis and b unit towards Y-Axis. And c unit is parameter of positioning the line on the Axis.

Axis Graph picture

Now you can see the meaning of a and b, x and y and the meaning of c as constant. If two lines are parallel and constant means the values of c is different then the lines could be parallel.

i.e. ax+by+9=0 and ax+by+5=0 are parallel lines where a and b are denoting the direction and values in Axis graph.

Now if both the equations are same, the the equations are overlapping and unlimited points could be common in both the lines.

Remember - Two points are needed to draw a line. But the location of the points is defined only when we know the values of demonstration on the axis. For example, let P is a point in the axis, that could be anywhere on the axis. But if we denote P (4,2) that means P point is 4 unit towards X - Axis and 2 unit towards Y - Axis.

Now let, there are 2 points, P (4,2) and Q (2,2) then the length of the line is D = √(4-2)^2+(2-2)^2

And slop of the line,

m = y2-y1 / x2 -x1

And the line passes through these points is,

y-y1 = m (x-x1)

So, in next articles we will discuss about lines and points in details. Stay tuned with us and share this post to your study circle.